toy r1 implementation!
2025-02-04 · 9 min readreproduced an ~250 line r1 GRPO training script in <24hrs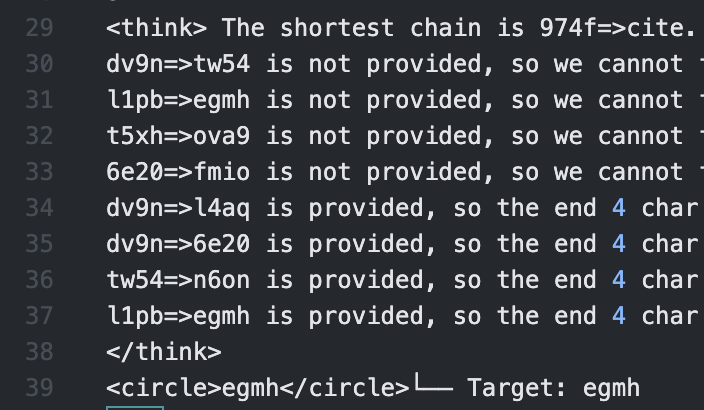
So I did what I did best, and made a quick reproduction of R1 in <250 lines!
Found some really interesting results on entropy in layers!!
After ablating LoRA layers and creating a new reasoning benchmark, I wanted to try new reasoning techniques! With GRPO and R1’s recent contributions, I wanted to 1) Reproduce cool aha! moments while training and 2) Have a good local environment to set up ablations.
I’m using my HashChain eval benchmark here , though any dataset can be swapped in/any reward function. The TLDR; for the task is to take in multiple chains of hashes and determine the shortest chain. Seemingly easy for a human, but once mixed up it gets quite hard.
The training recipe was mostly
-
Finetune with a LoRA lightly to align formatting generally, with random information inside the
tags. Used Qwen2.5-1.5b over here. - Start off the GRPO training & configure batch sizes/reward/group runoffs until it starts learning!
- Trained on 1 H100 in ~1hr! (open to any awesome way to get more compute)
You can check out the code over here—github.com/neelr/toy-r1
Some tips I have for people who want to train their own GRPO LLM models/things I learned:
- You can think of the group size vs the batch size as an explore vs exploit ratio (also the KL term). At least for me, since memory was a direct tradeoff, during the starting few steps a high group size worked great and then later a higher batch size/more gradient accumulation worked well.
- The KL term is extremely finicky and probably would benefit from some type of scheduling—it tends to blow up extremely easily. This is nice though because it stops your model from diverging too far from the mean.
- GRPO loss is distributed across all tokens—this is important otherwise your CoT weights won’t train, which is the most important part!
- This is definitely a lot more memory hungry than a SFT, which I assume makes parallel processing extremely important (possibly run quantized models for rollouts and maybe keep one set of master weights?)
- A model that is good at CoT is super important!!! I tried this with GPT2 and it couldn’t for coherent sentences and Qwen 0.5b was struggling. Larger models seem to have the prior necessary to “opt-out” of a value function with GRPO, which definitely seems really interesting (maybe if we have a smart enough model, we wouldn’t need backprop?)
- Formatting convergence was relatively fast ~100 steps, but convergence for the actual task was much much harder. Sparse rewards seem to do better, which is really surprising. The idea is that if your rollouts are somewhat near the correct answer, that provides a clear enough signal to “continue” on to the answer—vs noise of “slightly correct” answers.
interesting results
You can see that GRPO pretty significantly saturated accuracies on the high end (~5 chain) which you would expect to see with an RL workflow.
The entropy of the layers actually increased as GRPO steps increased! This is extremely interesting as I found similar results in reasoning paper, as reasoning skills seems to correlate with entropy. Really interesting because that means ELoRAs/maximizing entropy manually might give you similar boosts to r1.
Thanks to Niket for pointing this out to me on Qwen math!
Was able to reproduce the completion lengths increasing over time graph! Very cool, though initially I had to scaffold my formatting reward function to push “thoughts” inside the think tags. Even without rewards specifically incentivizing it, completion lengths got longer (which must mean its correlated with getting the answer right more!)
The loss curve definitely isn’t nice, but you see large drop offs whenever a new “reference” model is chosen for the KL loss. There is probably a lot of interesting temperature/learning rate warmup or cycling that could be done here to optimize learning.
Cool chain-of-thought dialogues I liked!
This one immediately struck me as cool, because it learned to write down the reconstruction of the hash list:
From the list of provided hashes, we can reconstruct the list as follows: tbi9=>mbr4, tbi9=>o8by, o8by=>1pb7, ai6x=>qz29, tbi9=>fcpq, 1pb7=>hrjh, qz29=>ho6a, mbr4=>ai6x. The task is to find the shortest chain and provide the end 4 char hash. The shortest chain is tbi9=>mbr4, mbr4=>ai6x, ai6x=>qz29, so the end 4 char hash is ho6a.
This definitely seemed a lot more english focused, which was really interesting:
The 9u5p is a list of multiple chains. The task requires us to reconstruct the list and find the shortest list. Since v4j6 is provided, we should focus on that. Since xxdt is the start, we can reconstruct the list backwards to 9u5p. We are looking for the list starting with xxdt. 9u5p was listed after pcay which was listed after j3cn, so we can reconstruct j3cn. After that, we can reconstruct the rest of the list. Since 0r9z is provided and 9u5p is listed after it, 9u5p is the end list.
Sometimes the best performing thoughts in the generation were things that I honestly didn’t understand quite well. It seems like its assigning new definitions to short here?:
To find the shortest chain, we should start with the most complex hash and work our way down. The shortest chain is 4ra1=>zwbq.
0uh7=>waao is not provided, so we can't find the end 4 char hash.
ojc1=>0uh7 is provided, so we can't find the end 4 char hash.
d5fd=>4ra1 is provided, so we can't find the end 4 char hash.
ojc1=>3sam is provided, so we can't find the end 4 char hash.
I’m always down to talk about anything! If you have any interesting thoughts feel free to email me @ neel.redkar@gmail.com
